旅行商|P vs. NP 五十年：AI正在解决不可解问题( 三 ) 电信|NTT|大阪世博会|6G|ntt|日本

Minicrypt：存在加密的单向函数的问题，但我们没有公钥加密

Cryptomania：公钥密码学，也就是说，两方可以通过公开渠道来交换加密信息，然后通过公钥解密

上述的5个层级没有正式的定义，都是通过人们对P和NP问题的了解人为规定的。但是人们普遍认为，Cryptomania这个等级的可能性最高。

Impagliazzo借鉴了P和NP理论中的核心思想——“我们无法拥有一切”。

我们或许可以解决困难的NP问题，或者解决密码学的重要关键，但是不能将两者同时攻克。

不过，也许我们正在走向事实上的Optiland——机器学习和软硬件优化等方面的长足进步让我们能够在一定程度上解决当年无法设想的问题，包括语音识别、蛋白质折叠解析等。但是大多数情况下，我们的密码协议仍然是安全的，所以不用太担心。

在2009年的综述中，我曾经在其中“如果P=NP怎么办”的章节中提出，通过使用奥卡姆剃刀法则，学习将会变得容易——我们只需要找到与数据一致的最小程序，也就是问题的关键核心。那么此时，原本十分难以解决的视觉识别、语音识别、翻译以及其他的任务都会变得微不足道。我们还将对天气、地震和其他自然现象做出更好的预测和理解，以及建模。

今天，我们可以使用人脸识别解锁手机，可以和一些智能设备语音对话来提出问题并且得到理想的回答，可以将我们说的话、输入的文字翻译成另外的语言。我们的手机会收到关于天气和其他突发事件的警报，它的预测效果比我们之前十几年前能做到的效果好的多。与此同时，除了对小密钥长度进行类似暴力破解的攻击之外，我们的密码学基本上还是很鲁棒和安全的。那么现在，让我们看看计算、优化和学习方面的最近进展如何将我们带到Optiland中吧！

解决困难问题

2016年，Bill Cook和他的同事决定挑战一个问题，就是如何以最短的距离访问英国的每一家酒吧。他们列出了已知的24727家酒吧，并且迈开腿，真的去走遍这些酒吧。这是一次跨越45495239米，大概28269英里的步行之旅，比绕地球一圈还要长。

其实Cook做了个弊，他没有真的走去每一家酒吧，他忽略了其中一些酒吧来让这次步行没那么夸张。这个事情在英国的媒体中宣传了之后，很多人在底下留言说：你没有来我家旁边的这个酒吧呀。于是，Cook和他的公司重新开始计划，将酒吧的名单增加到49687个，整体的旅行长度就达到了惊人的63739687米，也就是39606英里。但其实，相对于之前的那个旅行，这趟新的寻酒之旅其实只需要多走40%的距离就能达到两倍多数量的酒吧。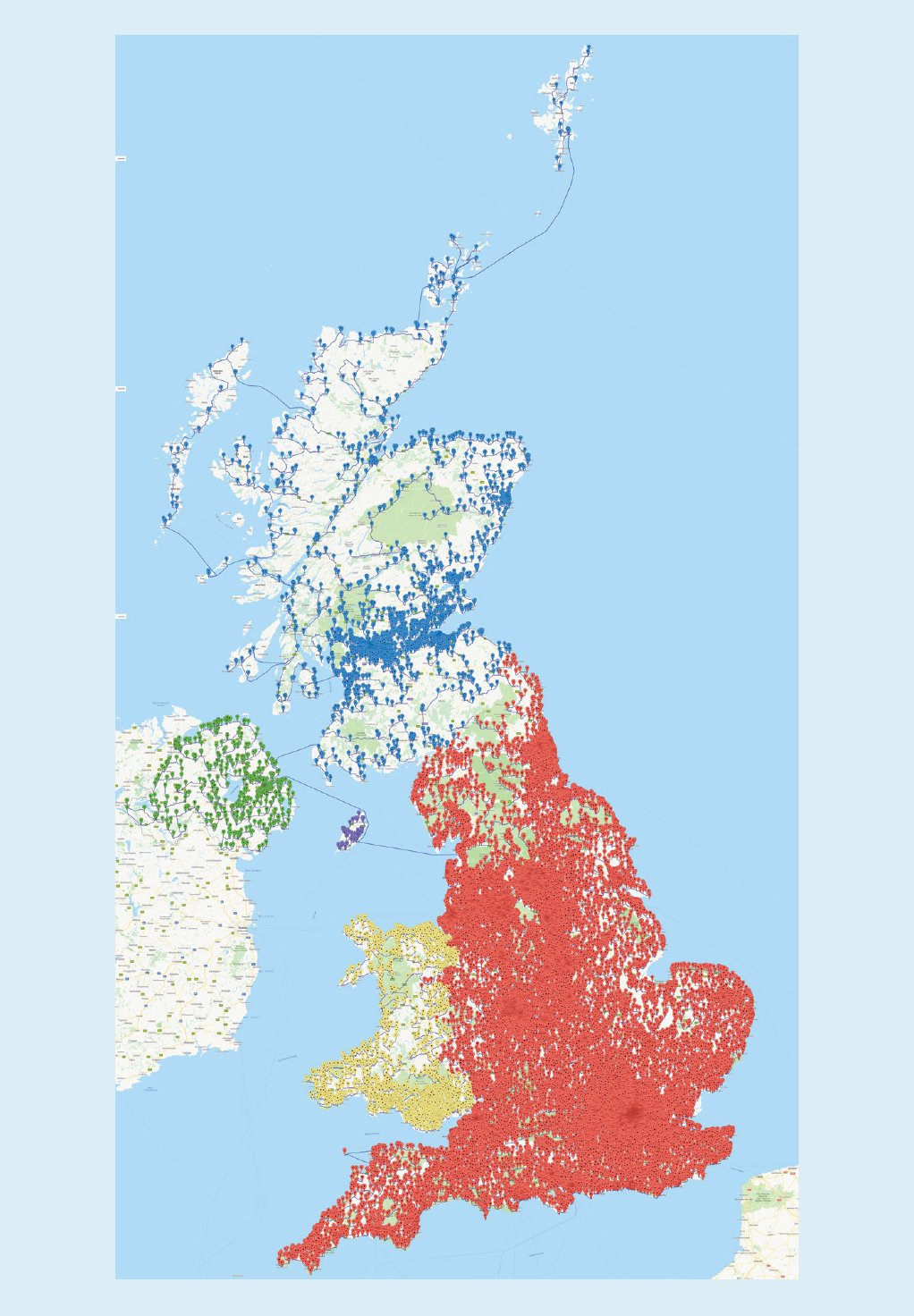

文章插图

遍历英国49687家酒吧的全览图

这种酒吧遍历之旅在某种程度上就是旅行商问题的变种，也就是最著名的NP完全问题之一。通过所有49687家酒吧的可能游览次数约等于3加上后面211761个零这个量级。当然了，Cook的计算机不会搜索整个集合，而是使用了多种优化的技术。更令人印象深刻的是，这次旅行带有基于线性程序对偶性的最优性证明。

除了旅行商问题之外，我们还看到了求解可满足性和混合整数规划方面的重大进步，也就是线性规划的一种变体，其中一些变量的解要求是整数。当我们使用高精度的启发式算法，使用快速的处理器、专用的硬件系统和分布式的云计算进行辅助的时候，人们通常可以解决实际中出现的具有好几万个变量和几十上百万个约束的问题。