物理课|《张朝阳的物理课》继续讨论热力学初谈熵概念( 三 ) 小巨人|余建平|新材料|阿里云

文章插图
另外，由于b到c以及d到a都是绝热膨胀，根据上节课推导的绝热方程可以得到：
将上述左边的等式除以右边的等式：

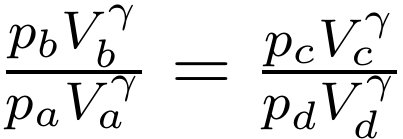
文章插图
再由abcd各点的理想气体状态方程可以得到：
那么联立上面的理想气体状态方程与绝热方程可以得到：

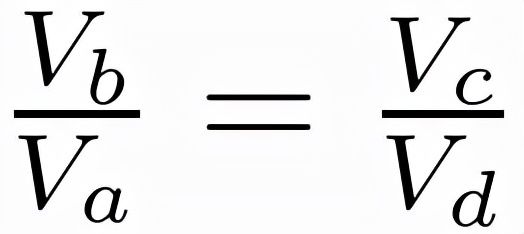
文章插图
利用此结论，最终可以确定Q2与Q1的比值与温度的关系为：

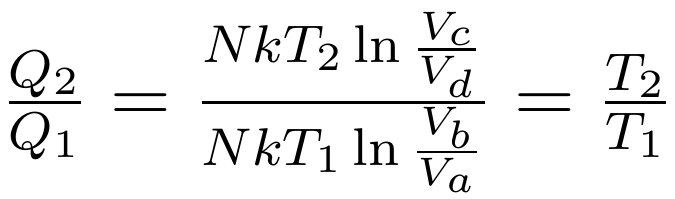
文章插图

文章插图
（计算理想气体作为热机工作物质时的热机效率）
“由此可见，热机的效率，确实只与两个热源的温度有关，并且利用开尔文温度表示出来具有非常简单的比值形式。”张朝阳边说边将公式改写为：

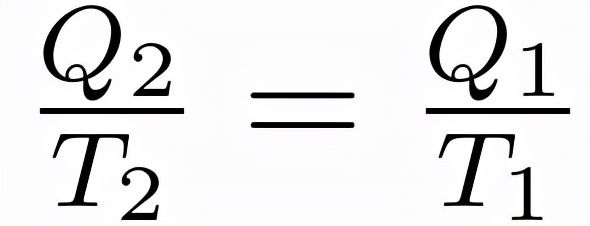
文章插图
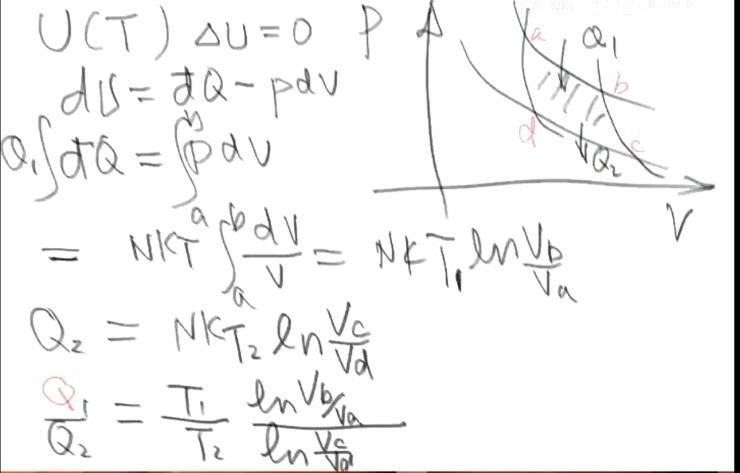
张朝阳根据此公式，引入熵的概念。他解释说，对于系统的任意一个准静态过程，选取其中某一微小过程，在这一微小过程中温度近似不变，设其为T，并在这个过程中它吸收了?Q的热量。我们可以引入一个辅助热源T'=1K与一个卡诺热机，此卡诺热机将系统看成热源，工作于系统与T'=1K的辅助热源之间，并且要求卡诺热机给温度为T的系统放出?Q的热量。设满足此条件的卡诺热机从辅助热源吸收了?Q'的热量，根据可逆热机效率与温度的关系可以得到?Q/T=?Q'/T'=?Q'/1K。对于其它微小过程同样也可以引入一个卡诺热机工作于系统与辅助热源之间。注意这里不同的卡诺热机工作于同一个T'=1K的辅助热源，这样积累成一个有限大过程之后，假设所有卡诺热机从辅助热源一共吸收了?Q'的热量，对应的系统的熵的变化可以定义为?S=?Q'/T'=?Q'/1K，由于辅助热源的温度为1K，其熵的变化数值上就等于这个辅助热源提供的总热量。若系统从状态a经过准静态过程到达状态b，用系统的温度与其吸收的热量来表示熵，熵还可以写为：

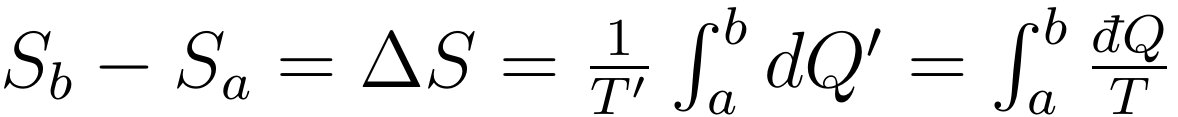
文章插图

文章插图
（张朝阳在介绍熵的定义）
“熵是一个状态函数，不与热过程有关，只与系统的状态有关。先看一个简单的例子，直观感受一下熵的概念。”张朝阳继续推导，考虑一个粒子数为N的理想气体从体积Vi自由膨胀到体积Vf的过程，这个过程不是准静态过程，所以不能直接套用上面关于熵的公式，但因为熵是个状态函数，它的变化只由气体的初始状态和末态决定，我们可以寻找一个准静态过程连接系统的初态与末态，就可以利用上述熵的计算公式计算出熵的变化。自由膨胀过程中理想气体不做功，气体内能不变，而理想气体内能只与温度有关，所以初态与末态的理想气体温度T不变，这样我们可以利用等温膨胀过程连接这个自由膨胀的初态与末态。前面已计算出等温膨胀时理想气体吸收的热量的表达式，代入上述熵的计算公式中即可得到熵的变化为：

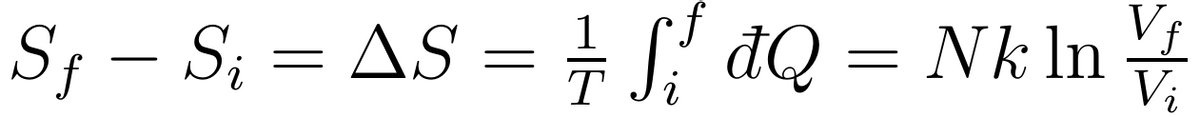
文章插图
网友们从他的推导中发现，容器体积从Vi膨胀为Vf时，理想气体里每个粒子可取的位置空间，变大为原来的Vf/Vi倍，直观地，相当于每个粒子可取的状态数Ω，也变大为原来的Vf/Vi倍。由于理想气体是近独立粒子系统，那么具有N个粒子的整个理想气体状态数，将变大为原来的(Vf/Vi)^N倍。若设初态与末态的气体状态数分别为Ωi与Ωf，则有：

物理课|《张朝阳的物理课》继续讨论热力学 初谈熵概念( 三 )

物理课|《张朝阳的物理课》继续讨论热力学初谈熵概念( 三 )