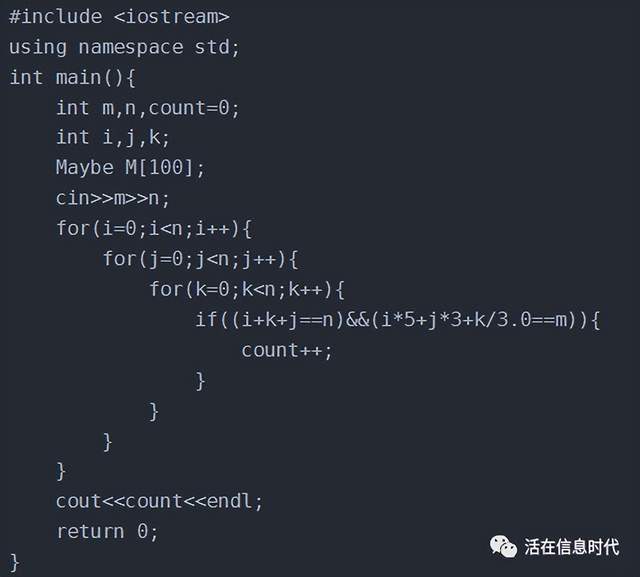
机器学习|程序员都应该精通的六种算法，你会了吗？算法

对于一名优秀的程序员来说，面对一个项目的需求的时候，一定会在脑海里浮现出最适合解决这个问题的方法是什么，选对了算法，就会起到事半功倍的效果，反之，则可能会使程序运行效率低下，还容易出bug 。因此，熟悉掌握常用的算法，是对于一个优秀程序员最基本的要求。
那么，常用的算法都有哪些呢？一般来讲，在我们日常工作中涉及到的算法，通常分为以下几个类型：分治、贪心、迭代、枚举、回溯、动态规划。下面我们来一一介绍这几种算法。
一、分治算法
分治算法，顾名思义，是将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。
分治算法一般分为三个部分：分解问题、解决问题、合并解。
分治算法适用于那些问题的规模缩小到一定程度就可以解决、并且各子问题之间相互独立，求出来的解可以合并为该问题的解的情况。
典型例子比如求解一个无序数组中的最大值，即可以采用分治算法，示例如下：
def dividAndConquer(arrleftIndexrightIndex):
if(rightIndex==leftIndex+1 || rightIndex==leftIndex){
return Math.max(arr[leftIndex
arr[rightIndex
);

int mid=(leftIndex+rightIndex)/2;
int leftMax=dividAndConquer(arrleftIndexmid);
int rightMax=dividAndConquer(arrmidrightIndex);
return Math.max(leftMaxrightMax);
二、贪心算法
贪心算法是指在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的仅是在某种意义上的局部最优解。
贪心算法的基本思路是把问题分成若干个子问题，然后对每个子问题求解，得到子问题的局部最优解，最后再把子问题的最优解合并成原问题的一个解。这里要注意一点就是贪心算法得到的不一定是全局最优解。这一缺陷导致了贪心算法的适用范围较少，更大的用途在于平衡算法效率和最终结果应用，类似于：反正就走这么多步，肯定给你一个值，至于是不是最优的，那我就管不了了。就好像去菜市场买几样菜，可以经过反复比价之后再买，或者是看到有卖的不管三七二十一先买了，总之最终结果是菜能买回来，但搞不好多花了几块钱。
典型例子比如部分背包问题：有n个物体，第i个物体的重量为Wi ，价值为Vi ，在总重量不超过C的情况下让总价值尽量高。每一个物体可以只取走一部分，价值和重量按比例计算。
贪心策略就是，每次都先拿性价比高的，判断不超过C 。
三、迭代算法
迭代法也称辗转法，是一种不断用变量的旧值递推新值的过程。迭代算法是用计算机解决问题的一种基本方法，它利用计算机运算速度快、适合做重复性操作的特点，让计算机对一组指令(或一定步骤)进行重复执行，在每次执行这组指令(或这些步骤)时，都从变量的原值推出它的一个新值。最终得到问题的结果。
迭代算法适用于那些每步输入参数变量一定，前值可以作为下一步输入参数的问题。
典型例子比如说，用迭代算法计算斐波那契数列。
四、枚举算法
枚举算法是我们在日常中使用到的最多的一个算法，它的核心思想就是:枚举所有的可能。枚举法的本质就是从所有候选答案中去搜索正确地解。
枚举算法适用于候选答案数量一定的情况。