神经网络|UC伯克利发现「没有免费午餐定理」加强版:每个神经网络,都是一个高维向量( 五 )
可学习性的统一形式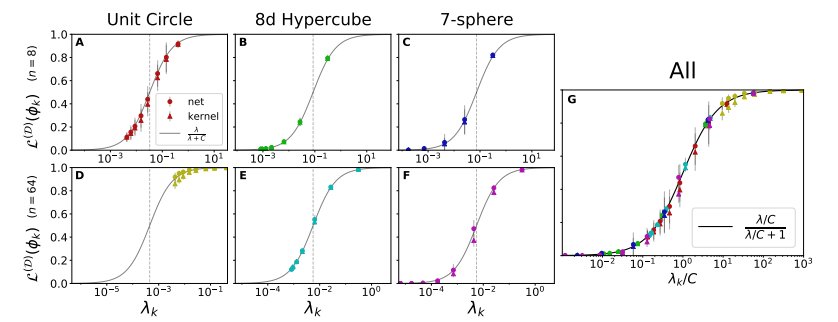
文章插图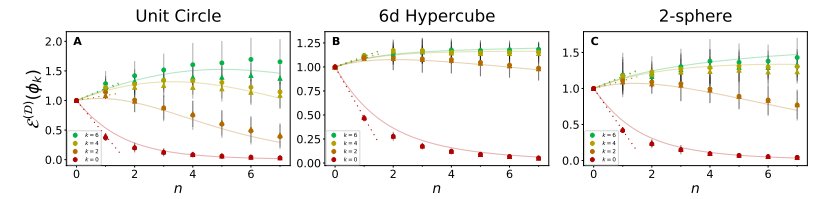
文章插图
MSE会随着数据点被加入到较小的训练集中而增大。(A-C)在给定的 n 个训练点的 3 个不同域上分别学习 4 个不同特征模时,NTK 回归和有限网络的泛化 MSE。理论曲线与实验数据非常吻合。
宽度有限网络下的情况
文章插图
上图显式了 8d 超立方体上的四个特征模式的可学习性和训练集大小的关系,作者使用了一个包含 4 个隐藏层的网络进行学习,其网络宽度可变,激活函数为 ReLU。所有图表中的理论曲线都相同,虚线表示了朴素的、泛化性能极差的模型的可学习性。(A)严格的 NTK 回归下的可学习性(B-F)有限宽度网络的可学习性。随着宽度的减小,平均的可学习性微弱增大, 1σ误差增大。尽管如此,即使在宽度仅仅为 20 时,平均学习率也与理论预测值十分契合。
对此,一作回应道:没错,我们的理论假设知道完整的目标学习函数 f^,而在实践中我们只能看到一个训练集。
“但从折中的角度来使用该理论也是可行的。假设我们知道目标学习函数属于少数可能函数之一。 该理论原则上包含足够的信息来优化内核,因此它在所有可能函数上都具有很高的平均性能。 当然,目标学习函数永远不会只是少数几个离散选项中的一个。但是如果拥有一些关于目标学习函数的先验——例如,自然图像可能服从某些统计。另外,或许也可以从数据-数据内核矩阵中获得足够的信息来使用该理论,我们以后可能会探索这个方向!”
- 5G|华为利用5G毫米波发现园区入侵者,这让美国5G联盟情何以堪
- 发现最小白矮星,其大小相当于月亮,这让科学家很兴奋
- 玉兔二号发现的“神秘小屋”前不久|玉兔二号拍到的月球背面的房子到底是什么,终于揭晓了
- Google|在德国留学发现,华为手机在欧洲市场相当于一块砖头
- 一斗穷、二斗富?康熙10个“簸箕”,科学家发现斗与簸箕的奥秘
- 微信|发现微信好友朋友圈是“一条杠”,删还不不删?
- 青年报·青春上海记者 陈嘉音/文 郭容/图、视频手办和雕像作为收藏品|青年发现|为中国人塑像,国风潮流玩具的“破圈”故事
- 揭开神秘面纱?嫦娥四号获取新成果:在月球背面发现“天外来客”
- 审查|德国监管机构:未发现任何证据表明小米手机具有“审查”功能
- 83年前宣布灭绝的鱼被发现还活着1月9日|83年前宣布灭绝的鱼被发现还活着,看似普通的它,为何难以发现
