|函数y=(4x+1)^2(x+11)的主要性质及其图像

文章图片
文章图片
函数y=(4x+1)^2(x+11)的主要性质及其图像主要内容:通过函数的定义域、值域、单调性、凸凹性及极限的性质 , 并通过函数导数知识求解函数的单调区间和凸凹区间 , 并简要画出函数y=(4x+1)^2(x+11)示意图的过程与步骤 。
※.函数定义域根据函y=(4x+1)^2(x+11)特征 , 可知函数自变量x可以取全体实数 , 即函数的定义域为:(-∞ , +∞) 。
※.函数一阶导数:本处通过导数工具来解析函数的单调性 , 过程如下:
∵y=(4x+1)^2(x+11) ,
∴y'=8(4x+1)(x+11)+(4x+1)^2 ,
=(4x+1)[8(x+11)+(4x+1)
=(4x+1)(12x+89)
令y'=0 , 有4x+1=0 , 12x+89=0 , 即:
x1=-4/4≈-0.3 , x2=-89/12≈-7.4.
(1).当x∈(-∞ , -7.4) , (-0.3+∞)时 ,
dy/dx>0此时函数为增函数 。
(2).当x∈[-7.4 , -0.3
时 ,
dy/dx<0此时函数为减函数 。
※.函数的凸凹性∵y'=(4x+1)(12x+89)
∴y''=4(12x+89)+12(4x+1)
=16(6x+23).
令y''=0 , 则6x+23=0 , 即:
x=-23/6≈-3.8.
此时函数的凸凹性性及凸凹区间为:
(1)当x∈(-∞ -3.8)时 , y''<0此时函数y为凸函数 。
(2)当x∈[-3.8+∞) 时 , y''>0此时函数y为凹函数 。
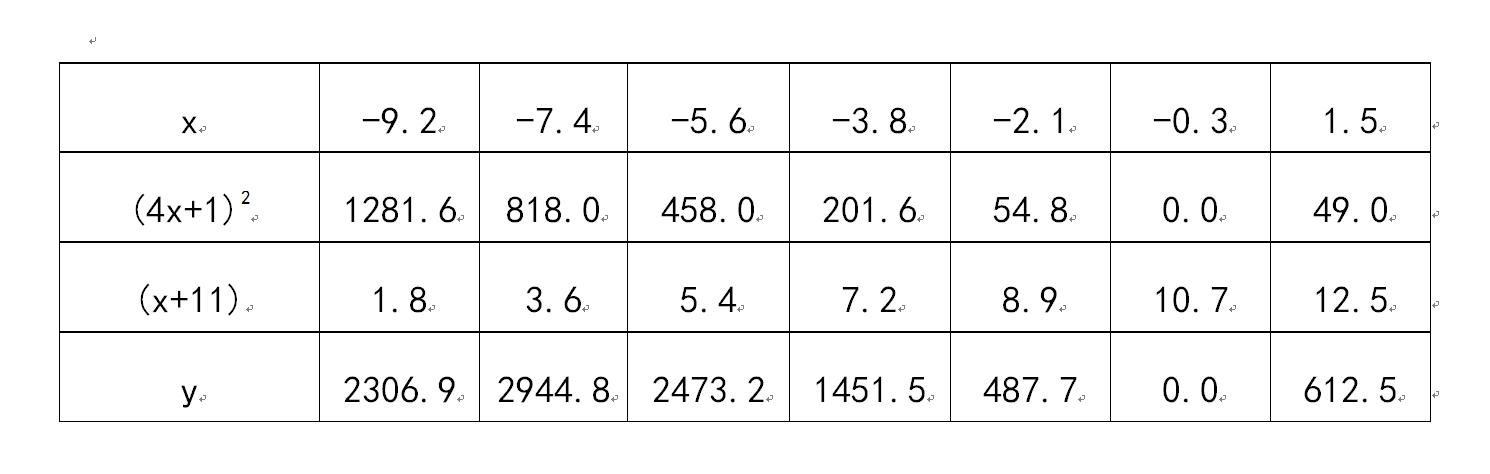
※.函数的部分点图
※.函数的图像示意图【|函数y=(4x+1)^2(x+11)的主要性质及其图像】
- |若与Lookup函数的这些经典用法牵手,就能轻松解决所有的查询问题
- 计算器科学数学函数计算,程序员16进制2进制逻辑运算图文教程
- 高中必考函数图像,手绘思维导图笔记,值得收藏
- |Vlookup实现不了的功能我用Xlookup函数实现,即简单,又高效!
- excel|当你与这几个函数公式成功牵手后,就会发现,原来Excel也很有趣
- excel|Excel中的多条件统计,掌握这几个函数公式就够了,收藏备用!
- |Office365中的这几个高能函数,正中使用痛点,用起来真香!
- 数据库|Office365中的这几个高能函数,正中使用痛点,用起来真香!
- |PyTorch常用5个抽样函数
- 今天希望通过一个小案例教会大家如何用Vlookup实现数据查询|vlookup函数:excel查询数据
